🧩🚀🔮 Mastering Functional JavaScript: Composition, Functors, and Monads Unveiled

Introduction

🚀 Today, we're going to talk about functional programming, which has become very popular among JavaScript developers. Simply put, functional programming is a paradigm where applications are composed using pure functions, avoiding shared mutable state and side-effects.

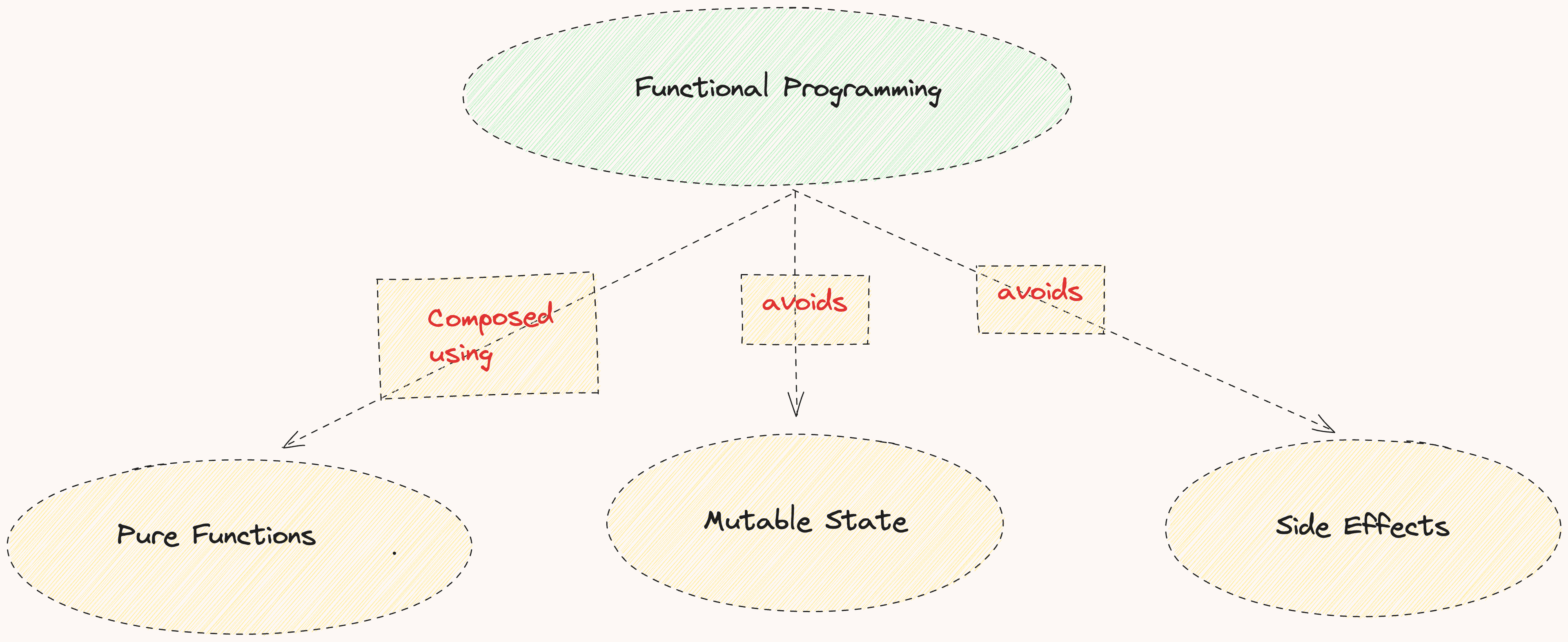
JavaScript has the most important features needed for functional programming:

• 1️⃣ First class functions: The ability to use functions as data values: pass functions as arguments, return functions, and assign functions to variables and object properties.
• 2️⃣ Anonymous functions and concise lambda syntax: x => x + 3 is a valid function expression in JavaScript.
• 3️⃣ Closures: When a function is defined inside another function, it has access to the variable bindings in the outer function, even after the outer function exits.

All three listed properties come from lambda calculus, which we will touch on in the next post, how it started and where the idea of lambda calculus came from. Functional programming is entirely based on the lambda calculus.

Functional programming is usually more declarative than imperative, meaning that we express what to do rather than how to do it. Functional code is more concise, more predictable, we are almost sure what the result will be and accordingly it becomes easier to test than arbitrary imperative or object-oriented code.

Let’s explain all the basic and significant concepts we have in functional programming.

• 🌟 Pure functions: A pure function is a function that, always returns the same outputs for the same input.For example in mathematics the pure function is

  math

  	sin(x)

  We know exactly and always that when x will be 30 degrees, the answer will be 1/2.

• 🛡️ No Side Effects: let's explain the first what is a side effect.Imagine that you are a child again. You are in the garden again and you are standing in front of a toy box with lots of toys: 🐣,🪱,🚨,🏍️,🎤. Each of them has its unique ability some make sounds, some light up, some move and some sing. Now let’s say you want to play with one of the toys, but when you take it out of the box and play with it, it affects other toys in the box. Maybe the toy makes a noise that startles the other toys, or maybe it moves around and knocks into other toys. This effect, in programming, we call a side effect, For adult children 🦾. It’s like a toy that has a special power that can affect other toys around it. Let’s bring examples of side effects that we understand:

  Examples of Side Effects :

  Making a network request

  Updating a database record

  Modifying the content of a file

• 🔀 Function Composition: This is the process when we combine one or more functions for some computation.For example, if we have a function g(x) and another function composition of them, it will be new function h(x) = f(g(x));

• 🌐 Shared state: It's a state which is shared between more than one function or more than one data-structure. When the state is immutable (can’t be changed), this is relatively harmless and is basically a memory-saving mechanism. If a shared state is mutable and used simultaneously by multiple threads, then the program will need to use locks or other mechanisms to operate on the state.

• 🗿 Immutability: Immutability is a key concept because without it we lose all the flow of states, and we lose the history of state changes.

Composition 🧩

Let’s consider an example of composition, let’s say we have 2 functions and we want to compose this functions.

	const f = n => n + 5;
	const g = n => n * 2;

Let's write a composition of this functions:

	const compose = x => f(g(x));

We know from algebra that (f ◦ g)(x) = f (g(x)), let's rewrite the compose function:

	const compose = (f,g) => x => f(g(x))

🔮 That's it. Now let us describe this union of functions in an even more general way, directly getting an array of functions as an argument.

	const compose = (...fns) => x => 
	   fns.reduce(
		(currentValue, currentFunction) => currentFunction(currentValue)
	   ,x);

No, let's play with this compose and compose some functions.

	const toUpper = str => str.toUpperCase();
	const exclaim = str => str + '!';
	const firstLetter = xs => xs[0];
 
	const loud  = compose(toUpper, firstLetter);
	const shout  = compose(loud,exclaim);
 
	console.log(shout("example"))// returns E!

I've created some functions and make a compositons, loud is composition of two functions and shout is composition of loud(which is a composition itself) and exclaim functions.

Composition is associative.In mathematics and computer science, a function or an operation is said to be associative if the way you group operations does not change the result. This means that if you have three or more items, it doesn't matter how they are grouped in pairs, the result will be the same. For example, let's consider addition, which is an associative operation. If you have three numbers, say 2, 3, and 4, you can add them in any order and you'll get the same result:

	(2 + 3) + 4 = 9
	 2 + (3 + 4) = 9

In both cases, the result is the same. This property is what makes addition associative. In the context of functional programming, a function f would be associative if for all inputs x,y, and z, the following holds true:

	f(f(x, y), z) = f(x, f(y, z))

In our example:

	compose(toUpper,firstLetter,exclaim) = 
		compose(compose(toUpper,firstLetter),exclaim) =
		 compose(toUpper,compose(firstLetter,exclaim))

Functors 🚂

In the simplest terms, a functor is a type that implements a map operation. In functional programming, it's a way to apply a function over or around some structure that we don't want to alter. The structure could be a list, a tree, or any other data structure - the important part is that the structure is not changed. Let's start with a normal function and then transform it into a functor.

// consider that large number is any number >= 20
const theFirstLargeNumber = xs => {
	const largeNumbers = xs.filter(x => x>=20);
	return largeNumbers[0];
}
console.log(theFirstLargeNumber[2,3,19,34,140,5]);//34

No, let's transform this solution into a functor way using the Box functor:

	const Box = (x) => ({
		map: f => Box(f(x)),
		fold: f => f(x)
	})

As we said functor implements a map function.

• ✔️ map: map method is a key characteristic of a functor. It applies a function to the value inside the functor and returns a new functor with the transformed value. The map method allows us to chain operations together in a clear and concise way. Here's a simple example:

  map-example.js

  	const box = Box(2);
  	const newBox = box.map(x => x * 2); // Box(4)

• ✔️ fold: I implemented a fold method just to extract the value from functor.

  fold-example.js

  	const box = Box(2);
  	const result = box.map(x => x * 2).fold(x => x); // 4

No, it's time to transform our function into a function way using Box functor.

	const Box = (x) => ({
		map: (f) => Box(f(x)),
		fold: (f) => f(x),
	});
 
	const theFirstLargeNumber = (xs) =>
		Box(xs)
		 .map(arr => arr.filter(x => x >= 20))
		 .fold(filtered => filtered[0]);
	
	console.log(theFirstLargeNumber([2,3,19,34,140,5])); // 34

Benefits of using functors

• 👌 Code clarity: Each operation is clearly separated, making the code easier to read and understand.

• ✅ Ease of modification: It's easy to add, remove, or modify operations without affecting the rest of the code.

• 🥷🏿 Error handling: Functors can be designed to handle errors in a consistent way, making your code more robust.

• 🎼 Composability: Functors can be easily composed together to create more complex operations.

Monads 🧙‍♂️

A monad is a type of functor that also implements a chain (also known as flatMap or bind) method. The chain method is used to sequence operations that return functors. In other words, a monad is a type of data type that wraps a value and provides two methods: map and chain. The map method is used to apply a function to the wrapped value and return a new monad. The chain method is used to "flatten" a nested monad.

Here's a simple example of a monad in JavaScript:

const Box = (x) => ({
	map: (f) => Box(f(x)),
	chain: (f) => f(x),
	fold: (f) => f(x),
});
 
const box = Box(2);
const newBox = box.chain(x => Box(x * 2)); // Box(4)
 

You see that The chain and fold methods in a monad do have similar structures, in that they both apply a function to the value inside the monad. However, the key difference lies in what they return and their purpose in the context of working with monads.

The chain method is particularly useful when you have a sequence of operations that each return a monad. For example, consider the following function that parses a string to a number and then increments it:

 
const Box = (x) => ({
	map: (f) => Box(f(x)),
	chain: (f) => f(x),
	fold: (f) => f(x),
});
 
const parseAndIncrement = (str) =>
	Box(str)
	 .map(s => parseInt(s))
	 .chain(n => Box(n + 1))
	 .fold(x => x);
console.log(parseAndIncrement("4")); // 5

In this example, map(s => parseInt(s)) transforms the string to a number and chain(n => Box(n + 1)) increments the number. Because the increment operation is wrapped in a Box, we use chain instead of map to avoid ending up with a Box inside a Box.

🛠️ Either Monad - Exapmle 1

Let's consider this function, that reads a package.json file and returns the dependencies from it.

	const getDependecies = () => {
		try {
			const str = fs.readFileSync("package.json");
			const config = JSON.parse(str);
			return config.dependencies;
		} catch (error) {
		return { 'error': error };
	}
};
 

First, create a Left and Right monads, sometimes referred to as the Either monad because a function can return either a Right value(representing success) or a Left value (representing failure).

const Right = (x) => ({
	chain: (f) => f(x),
	map: (f) => Right(f(x)),
	fold: (f, g) => g(x),
});
 
const Left = (x) => ({
	chain: (f) => Left(x),
	map: (f) => Left(x),	
	fold: (f, g) => f(x),
});
 

Let's break down it:

Right and Left Monads: The Right and Left functions create monads. The Right monad is used when a computation is successful, and the Left monad is used when there's an error. Both monads have chain, map, and fold methods, but they behave differently. For Right, map and chain apply the function to the value inside the monad. For Left, map and chain ignore the function and return the Left monad as is. The fold method for Right applies the second function (representing the success case), and for Left, it applies the first function (representing the error case).

No, we can create a utility tryCatch function to handle errors in a functionnal way.It will encapsulate operations that might throw exceptions and convert those exceptions into a manageable form.

	const Right = (x) => ({
		chain: (f) => f(x),
		map: (f) => Right(f(x)),
		fold: (f, g) => g(x),
	});
 
	const Left = (x) => ({
		chain: (f) => Left(x),
		map: (f) => Left(x),
		fold: (f, g) => f(x),
	});
 
	const tryCatch = (f) => {
	  try {
		return Right(f());
	  } catch (e) {
		return Left(e);
	  }
	};

Out tryCatch function provides a way to handle exceptions in a cleaner and more functional way. It takes a function f as an argument and tries to execute it. If f executes successfully, tryCatch returns a Right monad containing the result. If f throws an error, tryCatch catches the error and returns a Left monad containing the error.

Now, create a readFileSync 📂 function that will be a wrapper around the fs.readFileSync function. It uses tryCatch to read files, returning a Right monad on success or a Left monad on error, enabling consistent error handling.

const fs = require("fs");
 
const Right = (x) => ({
  chain: (f) => f(x),
  map: (f) => Right(f(x)),
  fold: (f, g) => g(x),
});
 
const Left = (x) => ({
  chain: (f) => Left(x),
  map: (f) => Left(x),
  fold: (f, g) => f(x),
});
 
const tryCatch = (f) => {
  try {
    return Right(f());
  } catch (e) {
    return Left(e);
  }
};
const readFileSync = (path) => 
		tryCatch(() => fs.readFileSync(path));
 

It's time to rewrite our core function:

const fs = require('fs');
 
const Right = (x) => ({
  chain: (f) => f(x),
  map: (f) => Right(f(x)),
  fold: (f, g) => g(x),
});
 
const Left = (x) => ({
  chain: (f) => Left(x),
  map: (f) => Left(x),
  fold: (f, g) => f(x),
});
 
const tryCatch = (f) => {
  try {
    return Right(f());
  } catch (e) {
    return Left(e);
  }
};
const readFileSync = (path) => tryCatch(() => fs.readFileSync(path));
 
const getDependencies = () =>
		 readFileSync("package.json")
		.chain((contents) => JSON.parse(contents))
		.map((config) => config.dependencies)
		.fold(
			(error) => ({ error: error }),
			(dependencies) => dependencies
);
const result = getDependencies();

• Step 1: Read the file "package.json". If successful, a Right monad with the file's contents is returned. If an error occurs, a Left monad with the error is returned.
• Step 2: If the previous operation was successful (i.e., we have a Right monad), parse the contents as JSON. If the parsing is successful, a new Right monad with the parsed object is returned. If the parsing fails, a Left monad with the error is returned. If the previous operation failed (i.e., we have a Left monad), this step is skipped.
• Step 3: If the previous operation was successful (i.e., we have a Right monad), extract the "dependencies" property from the parsed object. This returns a new Right monad with the dependencies. If the previous operation failed (i.e., we have a Left monad), this step is skipped.
• Step 4: Handle the result. If the previous operations were successful (i.e., we have a Right monad), return the dependencies. If any of the previous operations failed (i.e., we have a Left monad), return an object with the error.

How can we improve it❓

As you see, we're using JSON.parse and it can throw an error if contents is not valid JSON, and it doesn't return a monad. This could lead to unhandled exceptions and inconsistent behavior. We can improve it by using tryCatch function to handle potential parsing errors and ensure that we always return a monad.

Final Version 🪭

const fs = require('fs');
 
const Right = (x) => ({
  chain: (f) => f(x),
  map: (f) => Right(f(x)),
  fold: (f, g) => g(x),
});
 
const Left = (x) => ({
  chain: (f) => Left(x),
  map: (f) => Left(x),
  fold: (f, g) => f(x),
});
 
const tryCatch = (f) => {
  try {
    return Right(f());
  } catch (e) {
    return Left(e);
  }
};
const readFileSync = (path) => tryCatch(() => fs.readFileSync(path));
 
const parseJSON = (contents) => tryCatch(() => JSON.parse(contents));
 
const getDependencies = () =>
  readFileSync('package.json')
    .chain((contents) => parseJSON(contents))
    .map((config) => config.dependencies)
    .fold(
      () => 'No dependencies found',
      (dependencies) => dependencies
    );
const result = getDependencies();
 

📭🚪 Maybe Monad - Exapmle 2

I created a monad called Maybe that represents a value that may or may not be present. (null || undefined)

	const isNothing = (value) => value === null || value === undefined;
 
	const Maybe = (value) => ({
		map: (fn) => isNothing(value) ? Maybe.nothing() : Maybe.just(fn(value)),
		chain: (fn) => isNothing(value) ? Maybe.nothing() : fn(value),
		fold: (f, g) => isNothing(value) ? f() : g(value),
	});
 
	Maybe.just = (value) => Maybe(value);
	Maybe.nothing = () => Maybe(null);
 

map and chain methods are similar as previous ones. The fold method in the Maybe monad is used to extract the value from the monad. It takes two functions as arguments: f and g.

• ☑️ If the value inside the Maybe monad is null or undefined (checked by the isNothing function), it calls the function f with no arguments. This is typically used to provide a default value or handle an error case when the Maybe is nothing.
• ☑️ If the value inside the Maybe monad is not null or undefined, it calls the function g with the value. This is typically used to continue computations with the value when the Maybe is just. As you see we return a new Monad based on value we pass to it, if it's not present we return a Monad with null.

Let’s use this monad now. Let’s write a safeDivide function, which will accept dividend and divisor and return dividend/divisor. We will wrap it in the monad to avoid the side effect. In this case, the only side effect would be division by 0.

const isNothing = (value) => value === null || value === undefined;
 
  const Maybe = (value) => ({
  	map: (fn) => isNothing(value) ? Maybe.nothing() : Maybe.just(fn(value)),
 	chain: (fn) => isNothing(value) ? Maybe.nothing() : fn(value),
 	fold: (f, g) => isNothing(value) ? f() : g(value),
  });
 
Maybe.just = (value) => Maybe(value);
Maybe.nothing = () => Maybe(null);
 
function safeDivide(dividend, divisor) {
  if (divisor === 0) {
   	return Maybe.nothing();
  } else { 
  	return Maybe.just(dividend / divisor);
  }
}
 

Let us explain. If the divisor is 0, no division is possible and we return a new monad with no value, otherwise, we return a monad Maybe(dividend/divisor) with a new value.

Let’s look at a concrete example, and it will lead to a chain of several operations.

  const isNothing = (value) => value === null || value === undefined;
 
  const Maybe = (value) => ({
    map: (fn) => isNothing(value) ? Maybe.nothing() : Maybe.just(fn(value)),
    chain: (fn) => isNothing(value) ? Maybe.nothing() : fn(value),
    fold: (f, g) => isNothing(value) ? f() : g(value),
  });
 
  Maybe.just = (value) => Maybe(value);
  Maybe.nothing = () => Maybe(null);
 
  function safeDivide(dividend, divisor) {
	if (divisor === 0) {
		return Maybe.nothing();
	} else {
		return Maybe.just(dividend / divisor);
	}
  }
 
  const result = Maybe.just(2)
	.chain(x => safeDivide(10, x))
	.chain(x => safeDivide(100, x))
	.fold(
		() => `Error: division by zero`, 
		(res) =>res
	);
  console.log(result); // Output: 20
 

Example 3: List of users from the database

Imagine you want to retrieve a list of users from the database. This function can be disabled if an error occurred during a connection to the database or if the query fails. Come on, let’s put it in Monad and handle the side effects that way.

 
// Assume this function could fail due to a network error or other issue
const getUsers = () => {
	const users = [
		{ name: 'Alice', email:'alice@example.com' },
		{ name: 'Bob', email: 'bob@example.com' },
		{ name: 'Charlie', email: 'charlie@example.com' }
	];
	return Maybe.just(users);
}
 
// Retrieve the users and extract their names
const names = getUsers()
	.map(users => users.map(user => user.name))
	.map(names => names.map(name => name.toUpperCase()))
	.fold(() => [], (res) => res);
 
console.log(names);
// Output: ['ALICE', 'BOB', 'CHARLIE']

• getUsers() - returns a Maybe monad containing an array of user objects. Each user object has a name and an email.
• The first map method - applies a function to the array of users inside the Maybe monad. This function maps each user to their name, resulting in an array of names.
• The second map method - applies a function to the array of names inside the Maybe monad. This function maps each name to its uppercase version, resulting in an array of uppercase names.
• The fold method - is used to extract the array of uppercase names from the Maybe monad. If the Maybe monad is nothing (which would mean that getUsers() returned null or undefined), it returns an empty array. Otherwise, it returns the array of uppercase names.

Thanks for your attention! 🙌😊